인천대학교 이동선 교수, 상분리 및 상전이 현상에 대한 획기적 연구성과 발표
- 글번호
- 398449
- 작성일
- 2024-11-29
- 수정일
- 2024-12-10
- 작성자
- 홍보팀 (032-835-9490)
- 조회수
- 723

인천대 이동선 교수와 한국에너지공과대학교 김현주 교수 사진
인천대학교 수학교육과 이동선 교수와 한국에너지공대 김현주 교수는 시간-분수 차수 상태장 방정식(Time fractional phase-field equation)을 기반으로 서로 다른 물질이 연결되어 있는 도메인에서 상분리 현상을 해석함으로써 계산과학과 수치 시뮬레이션 분야에서 새로운 모델을 제시하는 연구논문을 발표하였다고 밝혔다.
상분리는 일반적으로 온도와 물질의 특성에 의해 영향을 받아 혼합물 내에서 서로 다른 상 (phase)이 분리되는 현상이다. 기존 연구에서는 상이 존재하는 도메인이 동질(homogeneity)해야 하므로 서로 다른 물질이 연결되어 있는 도메인 위에서는 어떠한 상분리가 일어나는가에 대해서는 계산할 수 없었다. 인천대 이동선 교수와 공동연구자인 김현주 교수는 이번 연구에서 다양한 시간-분수 차수를 적용한 알렌-칸(Allen-Cahn) 모델을 통해 각 면마다 다른 도메인 특질을 가지는 다면체 표면의 계산 영역에서 상분리 및 상의 기하적인 움직임을 연구하여 여러 물질이 결합되어 있는 도메인 위에서의 상분리 현상을 수치적으로 밝혀냈다.
특히, 이번 연구에서는 다면체 표면의 각 면마다 서로 다른 시간-분수 차수의 알렌-칸 모델를 적용함으로써 입자의 확산과 반응에 대해서 흥미로운 결과를 도출하였다. 이번 연구는 에너지 및 소재 공학 분야에서 정밀한 상 특성 제어와 반도체 설계에 중요한 과학적 기반을 제공하는데 기여할 것으로 기대된다.
이번 연구 결과는 응용수학 분야에서 피인용지수 상위 5%내에 속하는 Communications in Nonlinear Science and Numerical Simulation 학술지에 2024년 11월 19일자 온라인 판에 실렸다.
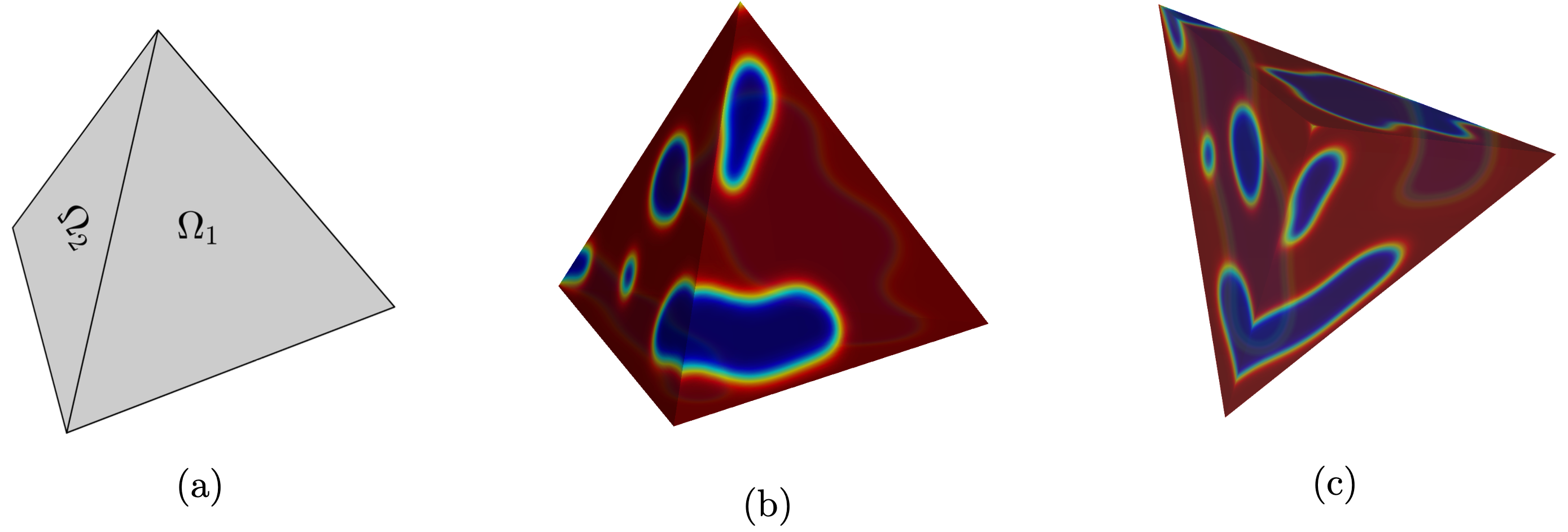
(a)는 사면체의 표면을 도메인으로써 나타낸다. (b)와 (c)는 각 면의 시간에 대한 미분 차수가 정수 차수로 동일한 경우로 동질한 도메인에서의 상분리 시뮬레이션 결과이다.
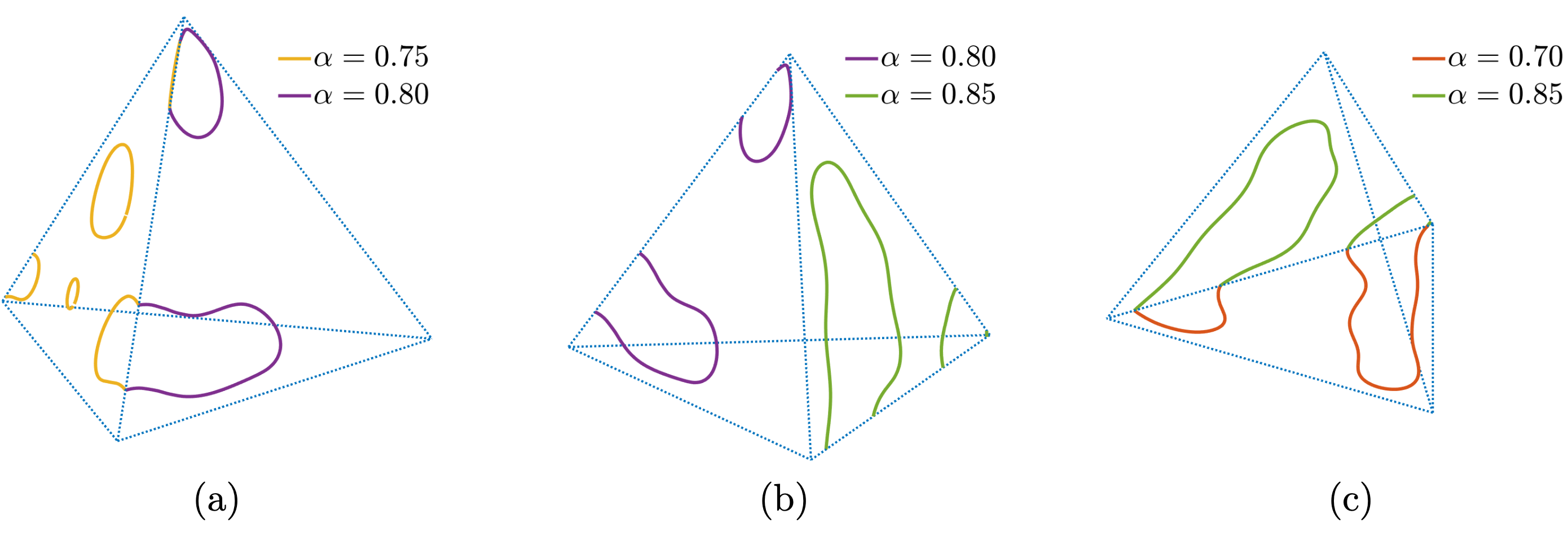
정사면체 각 면에 다른 시간-분수 차수를 적용했을 때 나타나는 상분리 현상에 대해 영수준 집합(zero-level set)만 나타낸 그림이다. 시간-분수 차수가 다른 이질적인 면 간 상분리 속도와 패턴이 달라지지만, 면 간 경계에서의 연속성은 유지되는 것을 볼 수 있다. 이는 다른 물질 특성을 가진 면들이 접합되었을 때도 자연스러운 상분리 패턴이 나타난다는 것을 의미한다.